This is a write-up of the presentation that Grace gave at Barcamp Bournemouth this weekend. I’ve written about the reaction she got already, but I thought her presentation was interesting enough that it’s worth sharing here.
The idea behind her talk was that the way maths is taught in schools today is different to the way it was done when I went to school.
Put another way, her basic premise was “when Dad helps me with my homework, he gets it all wrong”. 😉
Although, that’s a real point. Her teachers tell parents that if we try and get them to use methods that we learnt at school, that it could just confuse them, or worse: contradict what they learn in class. Some approaches are now thought to make it harder for children to learn essential maths concepts.
For example, I was taught to add a zero on the end to multiply something by 10. This causes problems when you get onto decimal numbers, when adding a zero on the end makes no difference. 3.4 multiplied by 10 isn’t 3.40.
This, and other techniques I learnt, aren’t used in Grace’s school any more, because of these sorts of reasons.
Instead, they are taught a series of techniques, starting with simple methods. As each method gets less effective at larger or more complex sums, they are taught another method that evolves the idea further.
In Grace’s talk, she went through the methods that they learn and how they are taught to write sums out.
Addition
Adding two numbers using…
Unstructured number line
Write your first number on the left of the line, and then jump to the right by the amount of your second number.
You do this in smaller jumps that are easier, basically in jumps of 10 until you get closer.
Partitioning
Partition each number into tens and units. Add them together separately, and then add the results.
I guess the point is that for now, separating the additions avoids having to do carry-overs.
Expanded column method
This is getting closer to how I learnt, but still they add the tens and units together separately, without the little carry-over numbers that I was taught to use.
Compensation
A bit different.
You round up the number you’re adding to something easier, then add that instead.
You then need to subtract the difference between the number you should have added and your rounded number, to compensate for the rounding.
Subtraction
Subtracting one number from another using…
Unstructured number line
Start at the right of the line, with your first number. And then jump left by the amount of your second number, doing it in smaller jumps that are easier to do (in hundreds or tens until you get closer).
Partitioning
Partition the second number into tens and units. Subtract the tens from the first number. And then subtract the units from the result as a second step.
Counting up
Start at the left of the number line with the number that you want subtract (the second number). And then jump up the number line until you reach the number you’re subtracting from (your first number).
The amount that you’ve had to jump to get there is the answer.
Compensation
You round up the number you’re subtracting to something easier, then subtract that instead.
You then need to add the difference between the number you should have subtracted and your rounded number, to compensate for the rounding.
Multiplication
Multiplying numbers using…
Arrays
Draw an array of dots, then count them. Only practical for small numbers, but it’s a way to make it clear how multiplication works.
Partitioning
Partition up the number to multiply, and then multiply them separately. Add up each of the results, using any of the addition methods above.
Grid method
Write out the sum in a grid, and do each bit separately.
One difference between what they do now and what I used to do is that the tens/hundreds/etc are still written out in full, to reinforce the message of the position.
Add up each of the results, using any of the addition methods above.
Short column method
Getting closer to how I used to learn long multiplication, multiplying each of the tens and units individually and then adding them together.
Division
Dividing numbers using…
Sharing
A very simple first method, imagining a number of people to share a collection of objects between. It doesn’t scale to very large numbers, but it’s how they start until they’re clear what division is.
Repeated subtraction
Subtract the number that you’re dividing by, repeatedly, until you reach zero. Then count the number of times you subtracted.
Chunking
Like repeated subtraction, but for larger numbers. You subtract multiples of the number you’re dividing by, instead of one at a time.
You can subtract any multiple you can think of, and keep doing that until you reach zero. Then you sum the multiples it took.
Inverse operation
They still spend a lot of time drilling the kids on times tables. So one approach they learn for division is reframing the sum as a multiplication with a missing value.
If they know the times-table answer, then they just know the answer. Otherwise, they learn to count up until they get to it.
And that’s it…
There are other techniques they learn, but those are the ones Grace got through in her talk.
Using a stylus and an iPad running Keynote connected to a projector, she went through the sums I’ve captured screenshots of here, explaining the idea as she went.
Just learned how 9 year-old Grace is taught how to do maths at school. Great talk and really interesting! #BCBOMO6 pic.twitter.com/5PyW3SRU6M
— Alex Washtell (@awashtell) May 10, 2014
As an aside, as a geeky presentation technique, it actually seemed pretty effective. I have to give it a try sometime – I’ve presented from an iPad before, but never scribbled on my slides while presenting!
Tags: school
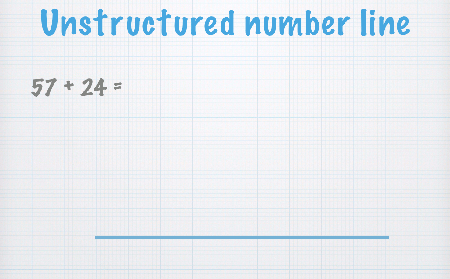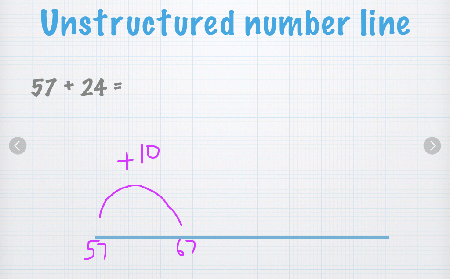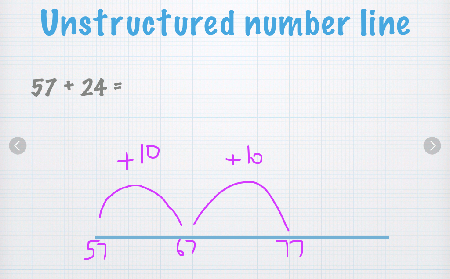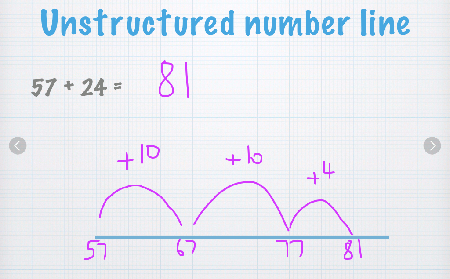















I’m not sure whether it is progress or just fashion. At our last infant school maths evening we were told that they are moving away from unstructured number lines back to addition in columns!
But do you think learning these techniques are good thing?
Some nice ideas there. I use compensation frequently in my head but usually for multiplication:
26*8 = 26*10 – 26*2 = 260 – 52
Not the best example of course because *8 is just repeated doubling, but there you go.
It’s interesting – there was a lot of debate at the barcamp after Grace’s talk, with the room being fairly divided as to whether these techniques are an improvement or not.
I don’t know how consistent this is between schools… I did have a quick look at the National Curriculum programme for maths in KS1/2 (https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study) and couldn’t see any explicit descriptions of methods, but I haven’t had a proper look through. It’d be interesting to know how much flexibility schools have, and how much variation there is between schools in the techniques taught.
I don’t remember ever doing number lines at school, but I think it might’ve helped me get my head around sums with positive/negative numbers, which I remember struggling with for quite a while as a kid. I think a number line would’ve helped me visualise it better.
Like Roger, I do think that some of them are closer to what I do in my head.
I found this really, really helpful to use when trying to explain methods to parents of neighbour’s children whom I tutor, same ages as your eldest two, and of course, near to you geographically. Well done Grace, an impressive task, obviously well executed.
thank you , it has helped me as a one who struggles with maths the step are easy for me to follow